Previous Post: A naive implementation of file-based storage
It was impossible to not come across B-Trees or any of the variants (B+Trees) if I had to implement a database. I hadn’t studied this data structure before.
Understanding the use case
At its core, B-Trees are multilevel indices for data stored in a database. A good introductory video of its structure and usage can be found here: https://www.youtube.com/watch?v=aZjYr87r1b8. I found Mr. Abdul Bari’s explanation easy to follow. A slightly discussion-oriented exposition can be found on Hussein Nasser’s channel: https://www.youtube.com/watch?v=UzHl2VzyZS4
Here is the crux of the problem—
Let’s say I need to retrieve data for some id=1008. How can I effectively get to the data?
- The brute-force approach is to read page by page. If our page-size is 1000, we will find our data on page 2. This is known as full-table scans.
- We can definitely optimise full-table scans by taking one or more of these approaches—
- Run multiple threads that scan for each page.
- Partition the table. For a given
id, data resides in a smaller sub-table. - Instead of scanning data tables, scan a metadata table (also known as index-table) and jump to the location.
It is not efficient to do full-table scans, and is downright impossible if the data is huge. The trick is to reduce the search space, not work with large dataset at all.
One option is to traverse through multiple layers of an m-ary tree, where each layer reduces the search space. B-Tree is one of the implementations of an m-ary tree where certain rules ensure that the tree is always balanced under mutation. The leaves, where the data is stored (or the pointer to the data), are disjoint. This poses a challenge while doing range queries. To traverse from one leaf to the next leaf, one must jump to its parent(s) and traverse the children(s).
B+Trees is an augmentation of B-Trees that connects one leaf node to the next one directly. It may seem trivial, but range-based queries are so ubiquitous that even MongoDB made a switch from B-Tree to B+Tree (WiredTiger) as its storage engine from version 3.2.
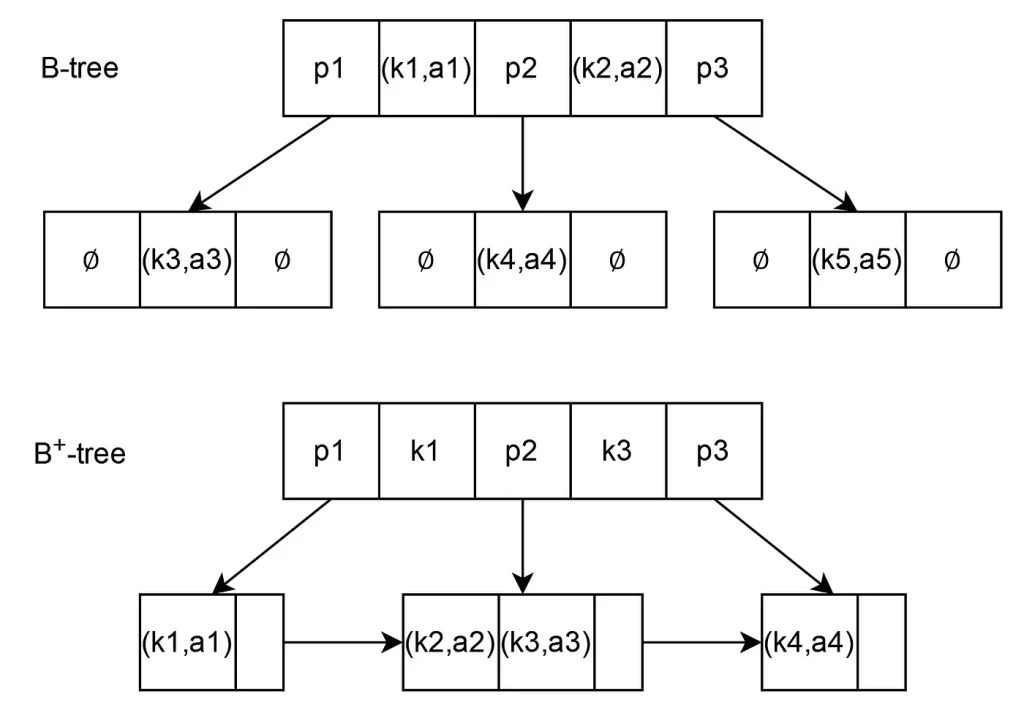
Image courtesy: Gianluca
Studying B+Tree algorithm
I wanted to take a shortcut and use a ready-made B+Tree Go library. Unfortunately, there isn’t one publicly available that I could rely on. I found an implementation by Collin Glass that is translated from Prof. Amittai Aviram’s C code. The translation had bugs. I ended up fixing the core functions after studying both codes side-by-side. The good part of this exercise was that I understood the implementation.
Along the way, I found a lovely B+Tree visualisation tool written by Prof. David Galles of USFCA: https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html (Please check out his page about visualisation of Algorithms. It’s terrific. There is one about B-Tree as well.)
The key thing is that having a B+Tree library is not enough. Having a B+Tree that is closely coupled with the storage schema and disk page is what enables efficient IO. This is where another book came to my rescue—James Smith’s Build Your Own Database from Scratch. Right as I dived into Chapter 04, I realised how important designing the low-level storage-schema (a.k.a wire-format) will be.
I took the idea and wrote a page library that is heavily inspired from James Smith’s book. Go’s builtin encoding/binary library did most of the heavy lifting in implementing trivial operations over a page’s serialised byte array.
State of code: https://github.com/sauvikbiswas/yeti/tree/01affd92bdaab2f37b497e8911384ba9d584390e
